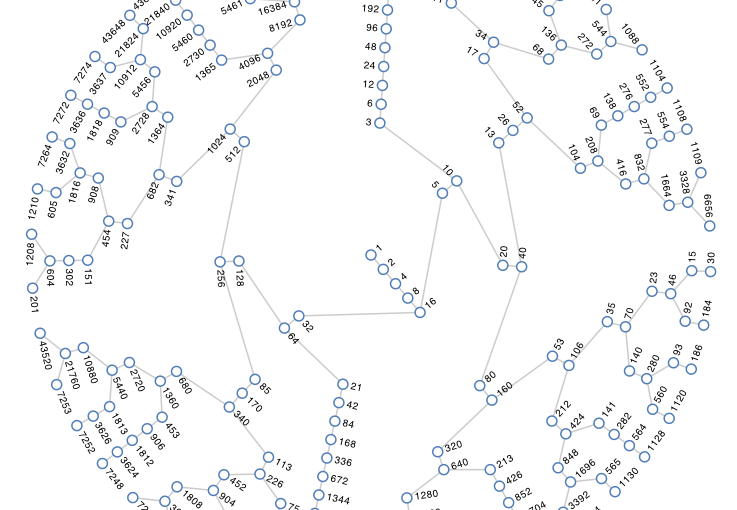
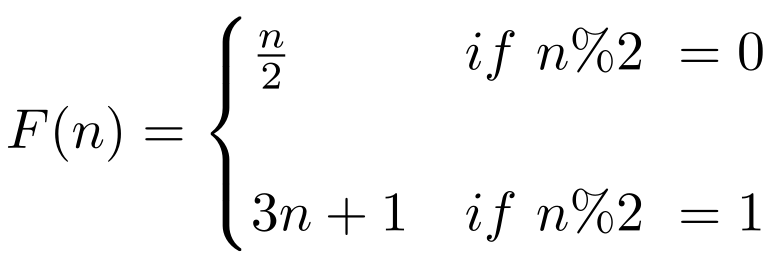LiD, and why you can become successful from studying goats.
Have you heard about LiD? It is the best concept ever to rise in education. A few years ago, professors in SFU gathered to discuss the idea of a broad education. They finally came with the conclusion that broad education sucks! And then, was born the concept of choosing one of dozens of highly interesting
Read More