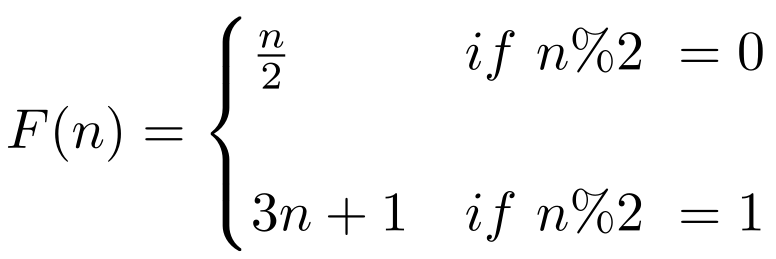Collatz Conjecture: The Unsolvable Problem
Recently I discovered a series of videos called Numberphile. I only watched two, both about a very interesting problem: the Collatz Conjecture. Imagine you take a number. If it is even, divide it by two, if it is odd, multiply it by three and add one. Take the next number and repeat. Simple, right? Let’s
Read More