Collatz Conjecture: The Unsolvable Problem
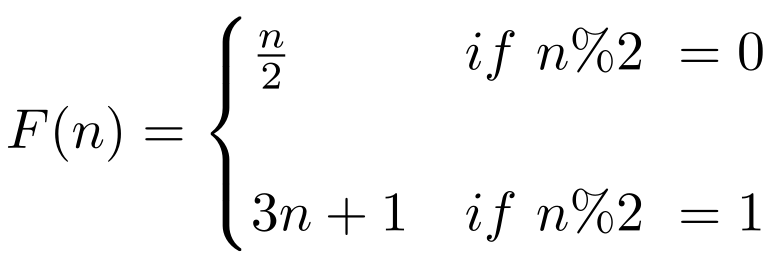
Recently I discovered a series of videos called Numberphile. I only watched two, both about a very interesting problem: the Collatz Conjecture.
Imagine you take a number. If it is even, divide it by two, if it is odd, multiply it by three and add one. Take the next number and repeat. Simple, right?
Let’s try it with the number 7.
3 * 7 + 1 = 22
22 / 2 = 11
3 * 11 + 1 = 34
34 / 2 = 17
3 * 17 + 1 = 52
52 / 2 = 13
3 * 13 + 1 = 40
40 / 2 = 20
20 / 2 = 10
10 / 2 = 5
3 * 5 + 1 = 16
16 / 2 = 8
8 / 2 = 4
4 / 2 = 2
2 / 2 = 1
Let’s continue from 1, then.
3 * 1 + 1 = 4
4 / 2 = 2
2 / 2 = 1
The idea of the Collatz Conjecture is that it will always reach 1, and that once it reaches one, it will keep on looping 1,4,2,1,4,2 forever. Nobody knows why this phenomenon happens.
Another interesting problem comes from counting how many steps it takes to get from a certain number to 1 with the Collatz Conjecture. I wrote a program for it which you can see right here:
The problem is finding the pattern between the number and Collatz Conjecture operations. So far, no one has been able to, and some mathematicians think no one will.
Thanks for reading!
For a program which calculates the steps to get from a number to 1 using the Collatz Conjecture, click here.
Hi,
I read your post and I really liked that. It is interesting to see how 7 resists this much to diverge to 1. Seems like it needs 15 steps which are 2 times bigger than 7 itself (15 > 7*2). Now I am interested to know what is the smallest number which can resist up to 3 times of its size in getting back to 1? I am also interested to know which number smaller than 100 will have the longest path to 1 and how long is that path?
I wrote a program to answer both of your questions. It came with these results:
It took 118 steps to reach from 96 to 1 which is maximum steps for a number under 100.
27 is the smallest number to have number of steps more than 3 times the number.
Thanks Aryan, Good to know 🙂
By the way as far as I know the longest sequence less than 100 billion known today is for 75,128,138,247, which has only 1228 steps. Another interesting fact is that 0 breaks the rule by staying 0 in zero steps but how about negative numbers. Is this theorem stands for negative numbers?!